How to Construct De Bruijn Graph From Reads

• Research Article
• Open Access
• Published: sixteen June 2016

Read mapping on de Bruijn graphs

BMC Bioinformatics volume 17, Article number:237 (2016) Cite this article

• 7701 Accesses

• 28 Citations

• 42 Altmetric

• Metrics details

Abstract

Groundwork

Next Generation Sequencing (NGS) has dramatically enhanced our ability to sequence genomes, but not to gather them. In practice, many published genome sequences remain in the state of a large set of contigs. Each contig describes the sequence found along some path of the assembly graph, even so, the set of contigs does not record all the sequence information contained in that graph. Although many subsequent analyses can be performed with the set of contigs, one may ask whether mapping reads on the contigs is as informative as mapping them on the paths of the associates graph. Currently, one lacks practical tools to perform mapping on such graphs.

Results

Here, we propose a formal definition of mapping on a de Bruijn graph, analyse the problem complexity which turns out to be NP-complete, and provide a practical solution. Nosotros propose a pipeline called GGMAP (Greedy Graph MAPping). Its novelty is a procedure to map reads on branching paths of the graph, for which we designed a heuristic algorithm called BGREAT (de Bruijn Graph REAd mapping Tool). For the sake of efficiency, BGREAT rewrites a read sequence as a succession of unitigs sequences. GGMAP can map millions of reads per CPU hour on a de Bruijn graph built from a large set of human being genomic reads. Surprisingly, results evidence that up to 22 % more reads can be mapped on the graph but non on the contig set.

Conclusions

Although mapping reads on a de Bruijn graph is circuitous task, our proposal offers a practical solution combining efficiency with an improved mapping capacity compared to assembly-based mapping even for complex eukaryotic information.

Background

Next Generation Sequencing technologies (NGS) have drastically accelerated the generation of sequenced genomes. Withal, these technologies remain unable to provide a single sequence per chromosome. Instead, they produce a large and redundant gear up of reads, with each read beingness a piece of the whole genome. Because of this redundancy, information technology is possible to discover overlaps betwixt reads and to gather them together in order to reconstruct the target genome sequence.

Fifty-fifty today, assembling reads remains a complex job for which no single piece of software performs consistently well [one]. The assembly problem itself has been shown to be computationally difficult, more than precisely NP-hard [2]. Practical limitations arise both from the construction of genomes (repeats longer than reads cannot be correctly resolved) and from the sequencing biases (non-uniform coverage and sequencing errors). Applied solutions represent the sequence of the reads in an assembly graph: the labels along a path of the graph encode a sequence. Currently, nigh assemblers rely on two types of graphs: either the de Bruijn graph (DBG) for the brusk reads produced by the second generation of sequencing technologies [three], or for long reads the overlap graph (which was introduced in the Celera Assembler [4]) and variants thereof, similar the string graph [5]. So, the assembly algorithm explores the graph using heuristics, selects some paths and outputs their sequences. Due to these heuristics, the ready of sequences obtained, chosen contigs, is biased and fragmented because of complex patterns in the graph that are generated by sequencing errors, and genomic variants and repeats. The gear up of contigs is rarely satisfactory and is usually post-processed, for instance, past discarding curt contigs.

The well-nigh frequent computational job for analyzing a set of reads is mapping them on a reference genome. Numerous tools are available to map reads when the reference genome has the grade of a set up of sequences (e.g. BWA [half-dozen] and Bowtie [seven]). The goal of mapping on a finished genome sequence is to say whether a sequence can exist aligned to this genome, and in this case, at which location(due south). This is more often than not washed with a heuristic (semi-global) alignment procedure that authorizes a small edit or Hamming distance between the read and genome sequences. Read mapping process suffers from regions of low mappability [eight]. Repeated genomic regions may not be mapped precisely since the reads mapping on these regions have multiple matches. When a genome is represented equally a graph, the mappability issue is reduced, as occurrences of each repeated region are factorized, limiting the problem of multiple matches of reads.

When the reference is not a finished genome sequence, but a redundant ready of contigs, the situation differs. The mapping may correctly determine whether the read is found in the genome, only multiple locations may for instance non be sufficient to conclude whether several truthful locations exist. Conversely, an unfruitful mapping of a read may be due to an incomplete associates or to the removal of some contigs during post-processing. In such cases, we argue information technology may be interesting to consider the assembly graph as a (less biased and/or more than complete) reference instead of the set of contigs. Then mapping on the paths of this graph is needed to complement mapping on prepare of contigs. This motivates the pattern and implementation of BGREAT.

In this context, we explore the trouble of mapping reads on a graph. Adjustment or mapping sequences on sequence graphs (a generic term meaning a graph representing sequences forth its paths) has already been explored in the literature in different application contexts: assembly, read correction, or metagenomics.

In the context of assembly, once a DBG has been built, mapping the reads dorsum to the graph can aid in eliminating unsupported paths or in computing the coverage of edges. To our noesis, no applied solution has been designed for this task. Cerulean assembler [9] mentions this possibility, merely only uses regular alignment on assembled sequences. Allpaths-LG [ten] also performs a like job to resolve repeats using long noisy reads from 3rd generation sequencing techniques. Its process is not generic enough to suit the mapping of any read ready on a DBG. From the theoretical view betoken, the question is related to the NP-hard read-threading trouble (also termed Eulerian superpath problem [two, 11]), which consists in finding a read coherent path in the DBG (a path that tin can be represented as a sequence of reads equally defined in [5]). The assembler called SPADES [12] threads the reads against the DBG by keeping track of the paths used during construction, which requires a substantial corporeality of memory. Here, we propose a more general problem, termed De Bruijn Graph Read Mapping Problem (DBGRMP), equally we aim at mapping to a graph any source of NGS reads, either those reads used for building the graph or other reads.

Recently, the hybrid mistake correction of long reads using short reads has go a critical step to leverage the third generation of sequencing technologies. The error corrector LoRDEC [13] builds the DBG of the curt reads, and so aligns each long read against the paths of the DBG by computing their edit distance using a dynamic programming algorithm (which is slow for our purposes). For shorts reads correction, several tools that evaluate the k-mer spectrum of reads to correct the sequencing errors use a probabilistic or an exact representation of a DBG as a reference [14, 15].

In the context of metagenomics, Wang et al. [xvi] have estimated the taxonomic composition of a metagenomics sample by mapping reads on a DBG representing several genomes of closely-related bacterial species. In fact, the graph collapses similar regions of these genomes and avoids redundant mapping. Their tool maps the read using BWA on the sequence resulting from the random concatenation of unitigs of the DBG. Hence, a read cannot align over several successive nodes of the graph (ER: il y a un pb ce n'est pas vrai). Similarly, several authors have proposed to store related genomes into a unmarried, less repetitive, DBG [17–19]. However, almost of these tools are efficient simply when applied to very closely related sequences that result in flat graphs. The BlastGraph tool [19], is specifically dedicated to the mapping of reads on graphs, just is unusable on real world graphs (meet Results section).

Here, nosotros formalize the mapping of reads on a De Bruijn graph and show that it is NP-complete. Then we present the pipeline GGMAP and dwell on BGREAT, a new tool which enables to map reads on branching paths of the DBG (Section GGMAP: a method to map reads on de Bruijn Graph). For the sake of efficiency, BGREAT adopts a heuristic algorithm that scales upwardly to huge sequencing data sets. In Section Results, we evaluate GGMAP in terms of mapping capacity and of efficiency, and compare it to mapping on assembled contigs. Finally, nosotros talk over the limitations and advantages the of GGMAP and requite some directions of future work (Department Word).

Methods

We formally ascertain the problem of mapping reads on a DBG and investigate its complication (Department Complication of mapping reads on the paths of a DBG). Also, we advise a pipeline called GGMAP to map short reads on a representation of a DBG (Department GGMAP: a method to map reads on de Bruijn Graph). This pipeline includes BGREAT, a new algorithm mapping sequences on branching paths of the graph (Section BGREAT: mapping reads on branching paths of the CDBG).

Complexity of mapping reads on the paths of a DBG

In this section, we present the formal problem we aim to solve and bear witness its intractability. Start, we introduce preliminary definitions, then formalize the problem of mapping reads on paths of a DBG, called the De Bruijn Graph Read Mapping Problem (DBGRMP), and finally bear witness it is NP-complete. Our starting point is the well-known Hamiltonian Path Problem (HPP); we apply several reductions to evidence the hardness of DBGRMP.

Definition 1 (de Bruijn graph).

Given a set of strings S={r ₁,r ₂,…,r _n } on an alphabet Σand an integer k≥2, the de Bruijn graph of lodge k of S (d B Grand _k (S)) is a directed graph (V,A) where:

$${} \begin{array}{lll} V &=& \{d \in \Sigma^{thousand} | \exists i \in \{1,\ldots,n\}\ {such\ that}\ d\ is\ a\ substring\\ &&of\ r_{i} \in S\}, and\\ A &=& \{(\!d, d')\! \mid if\ the\ suffix\ of\ length\ one thousand - one\ of\ d\ is\ a\ prefix\\ &&of\ d'\}. \stop{array} $$

Definition 2 (Walk and Path of a directed graph).

Let G be a directed graph.

• A walk of 1000 is an alternating sequence of nodes and connecting edges of G.

• A path of 1000 is a walk of K without repeated node.

• A Hamiltonian path is a path that that visits each node of G exactly once.

Definition iii (Sequence generated by a walk in a d B M _chiliad ).

Let G be a de Bruijn graph of order k. A walk of G equanimous of l nodes (v ₁,…,five _l ) generates a sequence of length g+50−1 obtained by the chain of v ₁ with the concluding character of v _ii, of v ₃,…, of five _l .

Nosotros ascertain the de Bruijn Graph Read Mapping Problem (DBGRMP) as follows:

Definition 4 (De Bruijn Graph Read Mapping Problem).

Given

• S, a set of strings over Σ,

• thousand, an integer such that k≥2,

• q:=q _i…q _|q| a word of Σ ^∗ such that |q|≥k,

• a toll function \(F : \Sigma \times \Sigma \rightarrow \mathbb {North}\), and

• a threshold \(t\in \mathbb {N}\),

decide whether there exists a path of the d B G _chiliad (S) composed of |q|−k+1 nodes (generating a word thousand:=yard ₁…yard _|q| ∈ Σ ^|q|) such that the cost \(C(one thousand,q) := \sum _{i=1}^{{\vert q \vert }} F(m_{i},q_{i}) \leq t\).

We recall the definition of the Hamiltonian Path Problem (HPP), which is NP-complete [twenty].

Definition 5 (Hamiltonian Path Problem (HPP)).

Given a directed graph G, the HPP consists in deciding whether there exists a Hamiltonian path of M.

To testify the NP-completeness of DBGRMP we introduce two intermediate problems. The first trouble is a variant of the Asymmetrical Travelling Salesman Problem.

Definition six (Fixed Length Disproportionate Travelling Salesman Problem (FLATSP)).

Let

• 50 be an integer,

• G:=(Five,A,c) exist a directed graph whose edges are labeled with a not-negative integer cost (given past the function \(c : A \rightarrow \mathbb {Northward}\)),

• \(t \in \mathbb {N}\) be a threshold.

FLATSP consists in deciding whether at that place exists a path p:=(v ₁,…,v _l ) of G composed of fifty nodes whose cost \(c(p) := \sum _{j = ane}^{l-1} c((v_{j},v_{j+1}))\) satisfies c(p)≤t.

Nosotros consider the brake of FLATSP to instances having a unit of measurement cost part (i.east., where c(a)=1 for any a ∈ A) and where l equals both the threshold and the number of nodes in V. This restriction makes FLATSP very similar to HPP, and the hardness effect quite natural.

Proposition 1.

FLATSP is NP-complete even when restricted to instances with a unit toll function and satisfying l=|V|=t.

Proof.

We reduce HPP to an instance of FLATSP where the cost role c simply counts the edges in the path, and where the path length 50 equals the threshold t and the number of nodes in 5.

Allow 1000=(V,A) exist a directed graph, which is an instance of HPP. Permit H=(V,A,c:A→{one}), and l:=|V| and t:=l. Thus (H,50,t) is an example of FLATSP.

Permit united states of america at present prove that there is an equivalence between the being of a Hamiltonian path in M and the being of a path p=(v ₁,…,five _fifty ) of H such that c(p)≤t. Assume that G has a Hamiltonian path p. In this instance, p is also a path in H of length |V|, and and so the toll of p equals its length, i.e. \(c(p) = \sum _{i=one}^{\vert V \vert } 1 = \vert 5 \vert \). Hence, there exists a path p of H such that c(p)≤t=|V|.

Presume that there exists a path p=(5 ₁,…,five _|V|) of H such that c(p)≤t. As p is a path it has no repeated nodes, and every bit past assumption fifty=|V|, one gets that p is a Hamiltonian path of H, and thus also a Hamiltonian path of 1000, since G and H share the same set of nodes and edges.

The second intermediate problem is chosen the Read Graph Mapping Trouble (GRMP) and is defined below. It formalizes the mapping on a general sequence graph. Hence, DBGRMP is a specialization of GRMP, since it considers the example of the de Bruijn graph.

Definition 7 (Graph Read Mapping Problem).

Given

• a directed graph G=(5,A,x), whose edges are labeled past symbols of the alphabet (x:A→Σ),

• q:=q _ane…q _|q| a discussion of Σ ^∗ ,

• a cost function \(F : \Sigma \times \Sigma \rightarrow \mathbb {N}\),

• a threshold \(t \in \mathbb {North}\),

GRMP consists in deciding whether at that place exists a path p:=(5 ₁,…,v _|q|+1) of G equanimous of |q|+one nodes, which generates a word one thousand:=m _i…m _|q| ∈ Σ ^|q| such that g _i :=x((five _i ,five _i+one)), and which satisfies \(\sum _{i=1}^{\vert q \vert } F(m_{i},q_{i}) \leq t\). Hither, grand is called the word generated past p.

Proposition two.

GRMP is NP-complete.

Proof.

We reduce FLATSP to GRMP.

Let \((G = (Five,A,c:A\rightarrow \mathbb {Northward}),l \in \mathbb {Due north},t \in \mathbb {Northward})\) be an example of FLATSP. Let Σ={y _i,…,y _|Σ|} an alphabet larger than the largest value of c(A), and let due south be the awarding such that s:{0,…,|Σ|}→Σ and such that for each i in {0,…,|Σ|}, s(i)=y _i . Let H=(5,A,ten:=s ∘ c) and let α exist a letter that does not belong to Σ, let q=α ^l−1 and F such that for each i in {0,…,|Σ|}, F(α,y _i )=i. Thus, we obtain |q|=l−1.

At present, let us show that in that location is an equivalence between the existence of a path p=(v ₁,…,5 ₅₀ ) of G such that c(p)≤t and the existence of a path p ^′=(u ₁,…,u _|q|+1) of H composed of |q|+i nodes, which generates a word m=thousand ₁…m _|q| of Σ ^|q|, where each thousand _j =x((u _j ,u _j+1)), and such that \(\sum _{j=one}^{\vert q \vert } F\left (m_{j},q_{j}\right) \leq t\). Presume that at that place exists a path p=(v ₁,…,five _l ) of M such that c(p)≤t. Past definition, p is a path in H. Permit m exist the word generated by p. Thus nosotros have \(\sum _{j=1}^{\vert q \vert } F\left (m_{j},q_{j}\right) = \sum _{j=1}^{l-1} F(m_{j},\alpha) = \sum _{j=one}^{50-i} c((v_{j}, v_{j+1})) \leq t\).

Now, suppose that there exists a path p ^′=(u ₁,…,u _|q|+1) of H equanimous of |q|+i nodes, which generates a word k=g ₁…m _|q| of Σ ^|q|, where each m _j =x((u _j ,u _j+i)), and such that \(\sum _{j=1}^{\vert q \vert } F\left (m_{j},q_{j}\right) \leq t\). By the construction of H, p ^′ is a path in G of length |q|+one=50. Hence, we obtain \(\sum _{j=one}^{50-i} c((u_{j}, u_{j+one})) = \sum _{j=ane}^{\vert q \vert } F(m_{j},\alpha) = \sum _{j=1}^{l-1} F\left (m_{j},q_{j}\right) \leq t\).

Theorem 1.

DBGRMP is NP-complete.

Figure one illustrates the gadget used in the proof of Theorem 1. Basically, the gadget creates a DBG node (a word) formed by concatening the labels of the ii preceding edges in the original graph.

Fig. 1

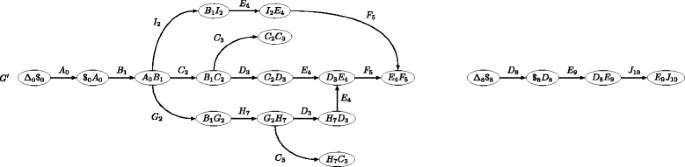
Illustration of the gadget used in the proof of Theorem 1. Encoding a directed graph into a DBG of gild 2. The directed graph 1000 (top) admits the aforementioned words than the ii-DBG G ^′ (bottom), if we ignore the numbers

Full size epitome

Proof.

Let us now reduce GRMP to DBGRMP.

Allow \((G := (5, A, x : A \rightarrow \Sigma),q \in \Sigma ^{\ast },F : \Sigma \times \Sigma \rightarrow \mathbb {North}, t\in \mathbb {Northward})\) be an instance of GRMP. Permit $ and Δ be two singled-out letters that practise not vest to Σ, and let Σ ^′:=Σ ∪{$,Δ}. Let 5 ^′ be a prepare of words of length two defined by

$${} \begin{array}{lll} V' := &\left\{ \alpha_{i} \beta_{j} \mid x(i,j) \right.\\ &\left.= \blastoff\ \text{and}\ \exists\ fifty \in V\ \text{such that}\ ten(j,l) = \beta\right\} & \qquad \mathbf{ready}\ ane\\ \bigcup \;\, &\left\{ \Delta_{i} \$_{i} \mid \exists\ j \in Five,\ \text{such that}\ x(i,j) \right.\\ &\left.= \alpha\ \text{and}\ \nexists\ l \in 5\ \text{such that}\ (l,i) \in A\right\} & \qquad \mathbf{ready}\ 2\\ \bigcup \;\, &\left\{ \$_{i} \alpha_{i} \mid \exists\ j \in V,\ \text{such that}\ x(i,j)\right. \\ &\left.= \alpha\ \text{and}\ \nexists\ l \in 5\ \text{such that}\ (50,i) \in A\right\}. & \qquad \mathbf{set}\ 3 \end{array} $$

(1)

Whatsoever letter of a discussion in V ^′ is a symbol of Σ ^′ numbered by a node of V. Moreover, if that symbol is taken from Five then it labels an border of A that goes out a node, say i, of Five, and the number associated to that symbol is i. In fact, V ^′ is the union of three sets (see Eq. 1):

set up ane considers the cases of an edge of A labeled α followed by an edge labeled β, sets ii and 3 contain the cases of an border of A labeled α that is not preceded by another edge of A; for each such border ane creates ii words: Δ _i $ _i in set 2 and $ _i α _i in set 3.

Let H exist the 2-dBG of V ^′; note that Σ ^′ is the alphabet of the words of V ^′. Now let z exist the application from 5 ^′ to Σ that for any α _i of V ^′ satisfies z(α _i )=α. (Note that in this equation, the correct term is a shortcut meaning the symbol of α _i without its numbering i; this shortcut is used only for the sake of legibility, but can be properly written with a heavier notation). Allow \(F' : \Sigma ' \times \Sigma \rightarrow \mathbb {North}\) be the application such that ∀(α _i ,β)∈ Σ ^′×Σ, F ^′(α _i ,β)=F(z(α _i ),β)=F(α,β).

Allow us testify that this reduction is a bijection that transforms a positive instance of GRMP into a positive instance of DBGRMP. Assume there exists a path p:=(five ₁,…,v _|q|+one) of G which generates a discussion m=m _i…m _|q| ∈ Σ ^|q| satisfying m _i =x((five _i ,v _i+1)) and such that \(\sum _{i=1}^{\vert q \vert } F(m_{i},q_{i}) \leq t\). We show that at that place exists a path p ^′ of M ^′ which generates a word grand ^′=grandane′…1000|q|′∈ Σ ^{′ |q|} such that \(\sum _{i=one}^{\vert q \vert } F'(m'_{i},q_{i}) \leq t\).

We build the path p ^′ equally the "chain" of two paths, denoted \(p^{\prime }_{offset}\) and \(p^{\prime number }_{terminate}\), that we ascertain below. Let \(\gamma _{j} := ten((v_{j},v_{j+ane}))_{v_{j}} = (m_{j})_{v_{j}}\phantom {\dot {i}\!}\) for all j between i and |q|. One has that γ _j ∈ Σ ^′. Now, let

$${} {p'_{start} := \left\{\!\!\! \begin{array}{fifty} \left(x((v_{50'},v_{fifty}))_{v_{fifty'}} ten((v_{l},v_{i}))_{v_{l}},\ x((v_{l},v_{1}))_{v_{50}}x((v_{1},v_{2}))_{v_{ane}} \right) \\ \quad \text{if}\ \exists\ l,l' \in V\ \text{such that}\ (l,ane) \in A\ \text{and}\ (l',l) \in A\\ \left(\$_{v_{l}} ten((v_{l},v_{1}))_{v_{l}},\ x((v_{50}, v_{1}))_{v_{l}} ten((v_{one}, v_{2}))_{v_{1}} \correct) \\ \quad \text{if}\ \exists\ \! l\! \in\! V\ \text{such that}\ \!(l,1\!)\! \in A\ \! \text{and}\ \! \nexists\ fifty' \in\! V\ \! \text{such that}\ (l',50) \in A \\ \left(\Delta_{v_{one}} \$_{v_{1}},\ \$_{v_{1}} x((v_{ane}, v_{2}))_{v_{i}} \right) \\ \quad \text{otherwise.} \finish{assortment}\correct.} $$

and let

$$p'_{finish} := \left(\gamma_{1} \gamma_{2},\ \ldots,\ \gamma_{\vert q \vert -1} \gamma_{\vert q \vert}\right). $$

Let m ^′ announce the word generated by p ^′. Clearly, one sees that \(\phantom {\dot {i}\!}k' = (m_{1})_{v_{i}} \ldots (m_{\vert q \vert })_{v_{\vert q \vert }}\), and since \(\phantom {\dot {i}\!}m_{i} = z((m_{i}')_{v_{i}})\), one gets that z(thou ^′)=m and \(\sum _{i=ane}^{\vert q \vert } F'\left (thou'_{i},q_{i}\right) = \sum _{i=i}^{\vert q \vert } F\left (m_{i},q_{i}\correct) \leq t\).

In the other direction, the proof is similar since our construction is a bijection.

GGMAP: a method to map reads on de Bruijn Graph

Nosotros propose a practical solution for solving DBGRMP. We consider the case of short (hundred of base pairs) reads with a low fault charge per unit (1 % of exchange), which is a proficient approximation of widely used NGS reads. Since errors are mostly substitutions, mapping is computed using the Hamming altitude.

Our solution is designed for mapping on a compacted de Bruijn graph (CDBG) any prepare of short reads, either those used to build the graph or reads from some other private or species. We recall that a CDBG is representation of a DBG in which each non branching path is merged into a unmarried node. The sequence of each node is called a unitig. Effigy 2 shows a DBG and the associated CDBG.

Fig. two

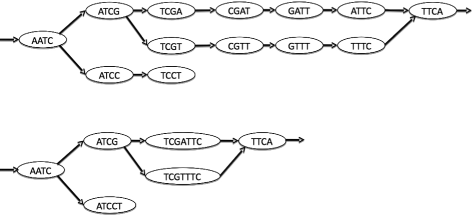
A toy case of a DBG of guild chiliad with k=4 (top) and its compacted version (lesser)

Full size prototype

In a CDBG, the nodes are not necessarily k-mers, words of length chiliad, merely unitigs, with some unitigs beingness longer than reads. Thus, while mapping on a CDBG, one distinguishes betwixt two mapping situations: i/ the reads mapping completely on a unitig of the graph, and ii/ the reads whose mapping spans 2 or more than unitigs. For the latter, we say that the read maps on a branching path of the graph.

Taking advantage of the extensive research carried out for mapping reads on flat strings, GGMAP uses Bowtie2 [seven] to map the reads on the unitigs. In improver, GGMAP integrates our proposed new tool, called BGREAT, for mapping reads on branching paths of the CDBG. Figure iii provides an overview of the pipeline.

Fig. 3

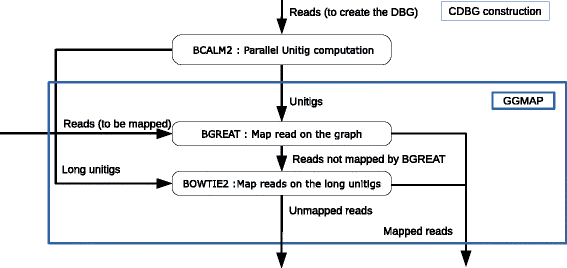
Unitig structure, as used in the proposed experiments (upper part of the figure) and GGMAP pipeline. Reads to be mapped tin can be distinct from reads used for edifice the graph. Long unitigs are unitigs longer than the reads. We remind that tools BCALM and BOWTIE2 are respectively published in [7, 21]

Total size image

GGMAP takes as inputs a query set of reads and a reference DBG. To avoid including sequencing errors in the DBG, we construct the reference DBG after filtering out all k-mers whose coverage lies beneath a user-defined threshold c. This fault removal step is a classical preprocessing step that is performed in m-mer based assemblers. The unitigs of the CDBG are computed using BCALM2 (the parallel version of BCALM [21]), using the k-mers having a coverage ≥c. GGMAP uses such a set of unitigs equally DBG.

We now propose a detailed description of BGREAT.

BGREAT: mapping reads on branching paths of the CDBG

As previously mentioned, BGREAT is designed for mapping reads on branching paths of a CDBG, using reasonable resources both in terms of fourth dimension and retentivity. Our approach follows the usual "seed and extend" prototype. More than generally, the proposed implementation applies heuristic schemes, both regarding the indexing and the alignment phases.

Indexing heuristic

Nosotros remind that our algorithm maps reads that span at least two distinct unitigs. Such mapped reads inevitably traverse i or more DBG edge(s). In a CDBG, edges are represented by the prefix and suffix of size k−1 of each unitig. We telephone call such sequences the overlaps. In order to limit the index size and the computation time, our algorithm indexes simply overlaps that are later used every bit seeds. Those overlaps are expert anchors for several reasons: they are long enough (one thousand−1) to exist selective, they cannot exist shared past more than than eight unitigs (four starting and four ending with the overlap), and a CDBG usually has a reasonable number of unitigs and then of overlaps. For instance, the CDBG in our experiment with human data has 70 million unitigs and 87 million overlaps for 3 billion m-mers). In our implementation, the index is a minimal perfect hash tabular array indicating for each overlap the unitig(s) starting or ending with this (k−i)-mer. Using a minimal perfect hash function limits the memory footprint, while keeping efficient query times (see Table 3).

Read alignment

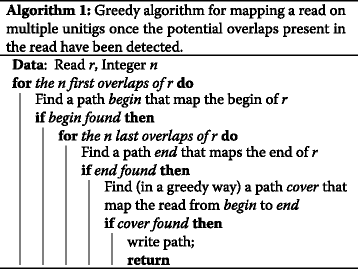
Given a read, each of its chiliad−1-mers is used to query the index. The alphabetize detects which k−1-mers represent an overlap of the CDBG. An example of a read together with the matched unitigs are displayed on Fig. 4. Once the overlaps and their corresponding unitigs accept been computed, the alignment of the read is performed from left to correct equally presented in Algorithm i. Given an overlap position i on the read, the unitigs starting with this overlap are aligned to the sequence of the read starting from position i. The best alignment is recorded. In addition, to improve speed, if 1 of the at most four unitigs catastrophe with the same overlap is the side by side overlap detected on the read, then this unitig is tested offset, and if the alignment contains less mismatch than the user defined threshold, the other unitigs are not considered. Note that this optimization does non apply for the first and last overlaps of a read.

Fig. 4

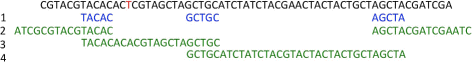
Representation of the mapping of a read (superlative sequence) on a CDBG, whose nodes are represented on lines ii, 3, and four. (step one) the overlaps of the graph that are also present in the read are institute (hither TACAC, GCTGC, and AGCTA, represented on line 1). (step 2) unitigs that map the beginning and the end of the read are found (those represented on line 2). (pace three) cover the balance of the read, guided past the overlaps (here with unitigs represented on lines three and four)

Total size image

This mapping procedure is performed only if the two extremities of the read are mapped by 2 unitigs. The extreme overlaps of the read enables BGREAT to quickly filter out unmappable reads. For doing this, the offset (resp. last) overlap of the read is used to align the read to the showtime (resp. terminal) unitig. Note that, as polymorphism exists between the read and the graph, some of the overlaps present on the read may be spurious. In this case the alignment fails, and the algorithm continues with the next (resp. previous) overlap. At about n alignment failures are authorized in each direction. If a read cannot be anchored neither on the left, nor on the correct, it is considered every bit not aligned to the graph.

Note that the whole approach is greedy: given two or more possible choices, the best 1 is chosen and backtracking is excluded. This results in a linear time mapping process, since each position in the read can lead to a maximum of four comparisons, and the algorithm continues as long as the cumulated number of mismatches remains below the user defined threshold. Because of heuristics, a read may exist unmapped or wrongly mapped for whatsoever of the post-obit reasons.

• All overlaps on which the read should map contain errors, in this case the read is not anchored or just badly anchored and thus not mapped.

• The due north first or n last overlaps of the read are spurious, in this case the begin or stop is not constitute and the read is not mapped. By default and in all experiments n=ii.

• The greedy choices made during the path selection are incorrect.

Nosotros implemented BGREAT as a dependence-costless tool in C++ available at github.com/Malfoy/BGREAT.

Results

Beforehand we give details almost the data sets (Subsection Data sets and CDBG construction), then we perform several evaluations of GGMAP and of BGREAT. Offset, we compare graph mapping to mapping on the contigs resulting from an associates (Subsection Graph mapping vs assembly mapping). Second, we assess how many reads are mapped on branching paths vs on unitigs (Subsection Mapping on branching paths usefulness). 3rd, we evaluate the efficiency of BGREAT in both terms of throughput and scalability (Subsection GGMAP performances), then appraise the quality of the mapping itself (Subsection GGMAP accuracy). All BGREAT alignments were performed authorizing up to two mismatches.

There are very few published tools to compare GGMAP with. Indeed, we found merely one published tool, called BlastGraph [19], which was designed for mapping reads on a DBG. However, on our simplest data set coming from the Eastward.coli genome (meet Table 1), BlastGraph crashed after ≈ 124 h of ciphering. Thus, BlastGraph was non farther investigated here.

Table ane CDBG used in this study

Full size table

Data sets and CDBG structure

For our experiments nosotros used publicly available Illumina read information sets from species of increasing complication: from the bacterium Due east.coli, the worm C.elegans, and from Man. Detailed information about the information sets are given in Additional file i: Table S1 (identifiers, read length, read numbers, and coverages – from 70x to 112x–).

For each of these iii data sets, we generated a CDBG using BCALM. From the C.elegans read fix, we additionally generated an artificially complex graph, past using pocket-sized k and c values (respectively 21 and ii). This particular graph, chosen C.elegans_cpx, contains lot of small-scale unitigs. Nosotros used it to appraise situations of highly complex and/or low quality sequencing data. The characteristics of the CDBG obtained on each of these data sets are given in Table 1.

Graph mapping vs assembly mapping

We compared GGMAP to the popular approach consisting in mapping the reads to the reference contigs computed by an assembler. For testing this arroyo, for each of the three sets used, we first assembled them and then we mapped back the reads on the obtained set of contigs. Nosotros used two dissimilar assemblers, the widely used Velvet [22], and Minia [23], a memory efficient assembler based on Bloom filters. Finally, nosotros used Bowtie2 for mapping the reads on the obtained contigs.

The results reported in Table 2 show that the number of reads mapped on assembled contigs is smaller than the one obtained with GGMAP. We obtained similar results in terms of number of reads mapped on the assemblies yielded by Velvet and Minia (see Additional file i: Table S2). Let us emphasize that on the Human dataset, GGMAP maps 22 additional percents of reads on the graph than Bowtie2 does on the assembly.

Table 2 Per centum of mapped reads, either mapping on contigs (here obtained thank to the Minia assembler) or mapping on CDBG with GGMAP

Total size table

We discover that the more than complex the graph, the higher the advantage of mapping on the CDBG. This is due to the inherent difficulty of assembling with huge and highly branching graphs. This is particularly prominent in the results obtained on the artificially complex C.elegans_cpx CDBG.

Nosotros too highlight that our approach is resources efficient compared to nigh assembly processes. For instance, Velvet used more 80 gigabytes of memory to compute the contigs for the C. elegans data set with thousand=31. On this data set, our workflow used at most 4 GB memory (during k-mer counting). In terms of throughput, using BGREAT and so Bowtie2 on long unitigs is comparable to using Bowtie2 on contigs alone. See Department GGMAP performances for more details well-nigh GGMAP performances.

Mapping on branching paths usefulness

Mapping the reads on branching paths of the graph is not equivalent to simply mapping the reads on unitigs. Indeed, at least 13 % of reads (mapping reads SRR959239 on the E.coli DBG) and upwards to 66 % of reads (mapping reads SRR065390 on C.elegans_cpx DBG) map on the branching paths of the graph (encounter Fig. five). These reads cannot be mapped when using only the set of unitigs as a reference. Equally expected, the more complex the graph, the larger the benefit of BGREAT'southward approach. On the complex C.elegans_cpx graph, only 23 % of reads can exist fully mapped on unitigs, while 89 % of them are mapped by additionally using BGREAT. On a simpler graph as C.elegans_norm the gap is smaller, simply remains significant (72 vs 93 %). Complete mapping results are shown in Boosted file 1: Table S3.

Fig. 5

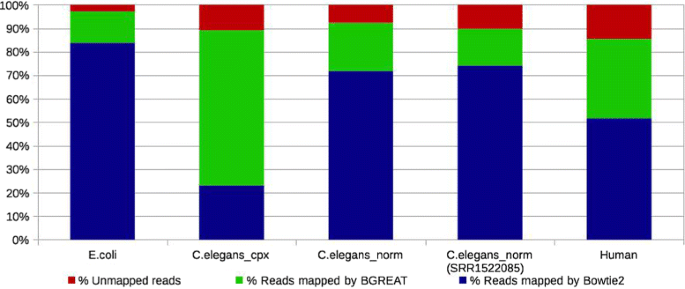
GGMAP mapping results for the different read sets. In the "C.Elegans_norm (SRR1522085)" case, reads from SRR1522085 are mapped on the CDBG obtained using reads from read set SRR065390. For all other results, the aforementioned read gear up was used both for constructing the CDBG and during the mapping

Full size prototype

Non reflexive mapping on a CDBG

The GGMAP approach is besides suitable for mapping a distinct read set from the one used for constructing the DBG. We mapped another read prepare from C.elegans (SRR1522085) on the C.elegans_norm CDBG. Results in this situation are similar to those observed when performing reflexive mapping (i.east., when mapping the reads used to construct this graph): among 89 % of mapped reads, 15 % were mapped on branching paths of the graph (Meet Fig. v).

GGMAP performances

Table 3 presents GGMAP fourth dimension and retentiveness footprints. It shows that BGREAT is very efficient in terms of throughput while using moderate resources. Presented heuristics and implementation details allow BGREAT to scale up to real-world instances of the problem, beingness able to map millions of reads per CPU hr on a Human CDBG with a depression memory footprint. BGREAT mapping is parallelized and can efficiently utilise dozens of cores.

Table 3 Fourth dimension and memory footprints of BGREAT and BOWTIE2

Total size table

GGMAP accurateness

To measure the touch of the read alignment heuristics, we forced the tool to explore exhaustively all potential alignment paths one time a read is anchored on the graph. Results on the E.coli dataset testify that the greedy approach is much faster than the exhaustive one (38 × faster), while the mapping capacity is little impacted: the overall number of mapped reads increases by only 0.03 % with the exhaustive approach. Nosotros thus claim that the choice of the greedy strategy is a satisfying trade-off.

To further evaluate the GGMAP accuracy, nosotros assess the retrieve and mapping quality in the following experiment. We created a CDBG from Human chromosome one (hg19 version). Thus, each k-mer of the chromosome appears in the graph. Furthermore, from the aforementioned sequence, we simulated reads with distinct mistake rates (0, 0.1, 0.2, 0.v, one and 2 %). For each mistake rate value, we generated one one thousand thousand reads. Nosotros evaluated the GGMAP results by mapping the imitation reads on the graph. Every bit the graph is fault gratis, except in some rare cases due to repetitions, the differences betwixt a correctly mapped read and the path information technology maps to in the graph occur at erroneous positions of the read. If this is not the example, nosotros say that the read is non mapped at its optimal position. Among the mistake free positions of a fake read, the number of mismatches observed between this read and the mapped path is called the "distance to optimal". Results are reported in Table 4 together with the obtained recall (number of mapped reads over the number of simulated reads). Those results show the limits of BGREAT while mapping reads from divergent individuals. With 2 % of substitutions in reads, merely 90.85 % of the reads are perfectly mapped. Even so, with this divergence rate, 97.28 % of reads are mapped at distance at nearly i from optimum. With over 99 % of perfectly mapped reads, these results bear witness that with the current sequencing characteristics, i.due east. a 0.one % error charge per unit, the mapping accuracy of BGREAT is suitable for most applications.

Table iv GGMAP mapping results on simulated reads from the reference of the human being chromosome 1 with default parameters

Total size table

Word

We proposed a formal definition of the de Bruijn graph Read Mapping Problem (DBGRMP) and proved its NP-abyss. Nosotros proposed a heuristic algorithm offering a practical solution. Nosotros developed a tool called BGREAT implementing this algorithm using a compacted de Bruijn graph (CDBG) as a reference.

From the theoretical viewpoint, the trouble DBGRMP considers paths rather than walks in the graph. The current proof of its hardness does not seem to be adjustable to the cases of walks. A perspective is to extend the hardness issue to that more general case.

We emphasize that our proposal does not enable genome annotation. It has been designed for applications aiming at a precise quantification of sequenced information, or a fix of potential variations between the reads and the reference genome. In this context, information technology is essential to map equally much reads every bit possible. Experiments evidence that a significant proportion of the reads (between ≈13and ≈66 % depending on the experiment) tin can be just mapped on branching paths of the graph. Hence, mapping just on the nodes of the graph or on assembled contigs is thus insufficient. This argument holds true when mapping the reads used for edifice the graph, only also with reads from a dissimilar experiment. Moreover, our results prove that a potentially large number of reads (upwards to ≈32%) that are mapped on a CDBG cannot be mapped on a classical assembly.

With GGMAP, the mapping quality is very high: using Human being chromosome 1 every bit a reference and reads with a realistic mistake rate (similar to that of Illumina engineering science), over 99 % of the reads are correctly mapped. The same experiment also pointed out the limits of mapping reads on a divergent graph reference (≥ii % substitutions): approximately ten % of the reads are mapped at a suboptimal position.

A weak indicate of BGREAT lies in its anchoring technique. Reads mapped with BGREAT must contain at least one exact k−ane-mer that is an arc of the CDBG, i.e., an overlap between two connected nodes. This may be a serious limitation when the original read set diverges greatly from the reads to exist mapped. Improving the mapping technique may exist washed by using non only unitig overlaps as anchors at the cost of higher computational resource. Some other solution may consist in using a smarter anchoring arroyo, similar spaced seeds, which can adjust errors in the anchor [24].

A natural extension consists in adapting BGREAT for mapping, on the CDBG obtained from short reads, the long (a few kilobases in average) and noisy reads produced by the third generation of sequencers, whose error charge per unit reaches upwards to xv % (with mostly insertion and deletion errors for due east.g. Pacific Biosciences technology). Such adaptation is non straightforward because of our seeding strategy, which requires long exact matches. The anchoring process must be very sensitive and very specific, while the mapping itself must implement a Blast-like heuristic or an alignment-free method. However, mapping such long reads on a DBG could be of interest for correcting these reads every bit in [thirteen], or for solving repeats, if long reads are mapped on the walks (which primary include cycles) of the DBG. Our NP-completeness proof only considers mapping on (acyclic) paths. Proving the hardness of the trouble of mapping reads on walks of a DBG remains open up.

Incidentally, using the same read fix for amalgam the CDBG and for mapping opens the fashion to major applications. Indeed, the graph and the exact location of each read on information technology may exist used for i/ read correction as in [15], by detecting differences between reads and the mapped area of the graph in which low support k-mers likely due to sequencing errors are absent, or for 2/ read compression past recording additionally the mapping errors, or for three/ both correction and compression past conserving only for each read its mapping location on the graph.

Having for each read (used for constructing the graph or not) its location on the CDBG also provides the opportunity to design algorithms for enriching the graph, for instance enabling a quantification that is sensitive to local variations. This would be valuable for applications such as variant calling, analysis of RNA-seq variants [25], or of metagenomic reads [26].

Additionally, BGREAT results provide pieces of information for distant k-mers in the CDBG, virtually their co-occurrences in the mapped read data sets. This offers a fashion for the resolution, in the de Bruijn graph, of repeats larger than k. Information technology could also allow to stage the polymorphisms and to reconstruct haplotypes.

Decision

A accept abode message is that read mapping can be significantly improved by mapping on the structure of an associates graph rather than on a set of assembled contigs (respectively ≈22 % and ≈32 % of additional reads mapped for the Human and a complex C.elegans information sets). This is mainly due to the fact that assembly graphs retains more than genomic information than assembled contigs, which also suffer from errors induced by the complexity of associates. Moreover, mapping on a compacted De Bruijn Graph can be fast. The availability of BGREAT opens the door to its awarding to key tasks such every bit read error correction, read compression, variant quantification, or haplotype reconstruction.

Abbreviations

CDBG, Compacted De Bruijn graph; DBG, De Bruijn graph; DBGRMP, De Bruijn graph read mapping problem; FLATSP, fixed length assymetric travelling salesman problem; GRMP, graph read mapping problem; HPP, Hamiltonian path trouble

References

1. Bradnam KR, Fass JN, et al.Assemblathon 2: evaluating de novo methods of genome associates in iii vertebrate species. GigaScience. 2013; two:x. [doi:10.1186/2047-217X-ii-x].

   Commodity  PubMed  PubMed Central  Google Scholar

2. Nagarajan N, Pop M. Parametric complexity of sequence assembly: theory and applications to next generation sequencing. J Comput Biol. 2009; 16(7):897–908. [doi:10.1089/cmb.2009.0005].

   CAS  Article  PubMed  Google Scholar

3. Chaisson MJ, Pevzner PA. Short read fragment associates of bacterial genomes. Genome Res. 2008; 18(2):324–xxx. [doi:x.1101/gr.7088808].

   CAS  Article  PubMed  PubMed Cardinal  Google Scholar

4. Myers EW, Sutton GG, et al.A whole-genome assembly of Drosophila. Scientific discipline (New York, N.Y.) 2000; 287(5461):2196–204. [doi:10.1126/science.287.5461.2196].

   CAS  Article  Google Scholar

5. Myers EW. The fragment associates string graph. Bioinformatics. 2005; 21(Suppl 2):79–85. [doi:10.1093/bioinformatics/bti1114].

   Commodity  Google Scholar

6. Li H, Durbin R. Fast and authentic short read alignment with Burrows-Wheeler transform. Bioinformatics. 2009; 25(14):1754–60. [doi:10.1093/bioinformatics/btp324].

   CAS  Commodity  PubMed  PubMed Central  Google Scholar

7. Langmead B, Salzberg SL. Fast gapped-read alignment with Bowtie ii. Nat Methods. 2012; 9(iv):357–9. [doi:10.1038/nmeth.1923].

   CAS  Article  PubMed  PubMed Central  Google Scholar

8. Lee H, Schatz MC. Genomic night matter: the reliability of brusk read mapping illustrated by the genome mappability score. Bioinformatics. 2012; 28(16):2097–105. [doi:ten.1093/bioinformatics/bts330].

   CAS  Article  PubMed  PubMed Central  Google Scholar

9. Deshpande Five, Fung EDK, Pham S, Bafna V. Cerulean: A Hybrid Associates Using High Throughput Curt and Long Reads. In: Lecture Notes in Reckoner Science vol. 8126 LNBI. Springer: 2013. p. 349–63, doi:10.1007/978-3-642-40453-5_27.

10. Ribeiro FJ, Przybylski D, Yin S, Sharpe T, Gnerre Southward, Abouelleil A, Berlin AM, Montmayeur A, Shea TP, Walker BJ, Immature SK, Russ C, Nusbaum C, MacCallum I, Jaffe DB. Finished bacterial genomes from shotgun sequence information. Genome Res. 2012; 22(11):2270–7. [doi:10.1101/gr.141515.112].

    CAS  Article  PubMed  PubMed Central  Google Scholar

11. Pevzner PA, Tang H, Waterman MS. An Eulerian path approach to Deoxyribonucleic acid fragment assembly. Proc Natl Acad Sci. 2001; 98(17):9748–53. [doi:10.1073/pnas.171285098].

    CAS  Commodity  PubMed  PubMed Cardinal  Google Scholar

12. Bankevich A, Nurk South, Antipov D, Gurevich AA, Dvorkin M, Kulikov AS, Lesin VM, Nikolenko SI, Pham Southward, Prjibelski Advertising, Pyshkin AV, Sirotkin AV, Vyahhi N, Tesler G, Alekseyev MA, Pevzner PA. SPAdes: a new genome assembly algorithm and its applications to single-cell sequencing. J Comput Biol. 2012; 19(5):455–77. [doi:10.1089/cmb.2012.0021].

    CAS  Article  PubMed  PubMed Key  Google Scholar

13. Salmela L, Rivals E. LoRDEC: authentic and efficient long read fault correction. Bioinformatics. 2014; thirty(24):3506–14. [doi:10.1093/bioinformatics/btu538].

    CAS  Article  PubMed  PubMed Central  Google Scholar

14. Yang X, Chockalingam SP, Aluru S. A survey of error-correction methods for next-generation sequencing. Brief Bioinform. 2013; 14(1):56–66. [doi:10.1093/bib/bbs015].

    CAS  Article  PubMed  Google Scholar

15. Benoit 1000, Lavenier D, Lemaitre C, Rizk G. Bloocoo, a memory efficient read corrector. In: European Conference on Computational Biological science (ECCB): 2014. https://gatb.inria.fr/software/bloocoo/.

16. Wang M, Ye Y, Tang H. A de Bruijn graph approach to the quantification of closely-related genomes in a microbial community. J Comput Biol. 2012; 19(6):814–25. [doi:10.1089/cmb.2012.0058].

    CAS  Article  PubMed  PubMed Key  Google Scholar

17. Huang L, Popic V, Batzoglou Southward. Short read alignment with populations of genomes. Bioinformatics. 2013; 29(thirteen):361–seventy. [doi:10.1093/bioinformatics/btt215].

    Article  Google Scholar

18. Dilthey A, Cox C, Iqbal Z, Nelson MR, McVean Grand. Improved genome inference in the MHC using a population reference graph. Nat Genet. 2015; 47(half-dozen):682–eight. [doi:x.1038/ng.3257].

    CAS  Article  PubMed  PubMed Cardinal  Google Scholar

19. Holley G, Peterlongo P. Blastgraph: Intensive guess pattern matching in sequence graphs and de-bruijn graphs. In: Stringology: 2012. p. 53–63. http://alcovna.genouest.org/blastree/.

20. Karp RM. Reducibility Among Combinatorial Bug. In: 50 Years of Integer Programming 1958-2008. Berlin, Heidelberg: Springer: 2010. p. 219–41. doi:10.1007/978-3-540-68279-0_8. http://link.springer.com/x.1007/978-three-540-68279-0_8.

    Google Scholar

21. Chikhi R, Limasset A, Jackman Southward, Simpson JT, Medvedev P. On the representation of de bruijn graphs. In: Research in Computational Molecular Biology. Springer: 2014. p. 35–55, doi:10.1007/978-3-319-05269-4-4.

22. Zerbino DR, Birney Eastward. Velvet: algorithms for de novo curt read assembly using de Bruijn graphs. Genome Res. 2008; 18(5):821–ix. [doi:x.1101/gr.074492.107].

    CAS  Article  PubMed  PubMed Fundamental  Google Scholar

23. Chikhi R, Rizk K. Space-efficient and verbal de Bruijn graph representation based on a Flower filter. Algorithm Mol Biol. 2013; viii(i):22. [doi:10.1186/1748-7188-8-22].

    Article  Google Scholar

24. Vroland C, Salson M, Touzet H. Lossless seeds for searching curt patterns with high mistake rates. In: Combinatorial Algorithms. Springer: 2014. p. 364–75.

25. Sacomoto GA, Kielbassa J, Chikhi R, Uricaru R, Antoniou P, Sagot MF, Peterlongo P, Lacroix V. Kissplice: de-novo calling alternative splicing events from rna-seq data. BMC Bioinformatics. 2012; xiii(Suppl 6):5.

    Google Scholar

26. Ye Y, Tang H. Utilizing de Bruijn graph of metagenome assembly for metatranscriptome analysis. Bioinformatics. 2015:btv510. Oxford Univ Press. arXiv preprint arXiv:1504.01304.

Download references

Acknowledgements

We would like to give thanks Yannick Zakowski, Claire Lemaitre and Camille Marchet for proofreading the manuscript and discussions.

Funding

This work was funded by French ANR-12-BS02-0008 Colib'read project, by ANR-11-BINF-0002, and by a MASTODONS project.

Availability of data and materials

Our implementations are available at github.com/Malfoy/BGREAT. In addition to the following pieces of data, Additional file one: Table S1 presents the master characteristics of these datasets.

SRR959239 http://www.ncbi.nlm.nih.gov/sra/?term=SRR959239

SRR065390 http://www.ncbi.nlm.nih.gov/sra/?term=SRR065390

SRR1522085 http://www.ncbi.nlm.nih.gov/sra/?term=SRR1522085

SRR345593 and SRR345594 http://world wide web.ncbi.nlm.nih.gov/sra/?term=SRR345593.

Authors' contributions

PP initiated the work and designed the written report. AL, BC and ER designed the ceremonial and the proofs of NP-hardness. AL designed the algorithmic framework, implemented the BGREAT and performed the tests. All authors wrote and accepted the concluding version of the manuscript.

Competing interests

The authors declare that they have no competing interests.

Ethics blessing and consent to participate

Not applicable.

Author information

Affiliations

1. IRISA Inria Rennes Bretagne Atlantique, GenScale team, Campus de Beaulieu, Rennes, 35042, French republic

   Antoine Limasset & Pierre Peterlongo

2. L.I.R.Thou.M., UMR 5506, Université de Montpellier et CNRS, 860 rue de St Priest, Montpellier Cedex 5, F-34392, France

   Bastien Cazaux & Eric Rivals

3. Institut Biologie Computationnelle, Université de Montpellier, Montpellier, F-34392, France

   Bastien Cazaux & Eric Rivals

Corresponding author

Correspondence to Antoine Limasset.

Additional file

Additional file 1

Read mapping on De Bruijn graphs additional file. Iii complementary tables are presented. Main characteristics of information sets used in this study. Assembly and mapping approach comparison. Results of BGREAT on real read sets. (PDF 40 kb)

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution iv.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted employ, distribution, and reproduction in any medium, provided you give advisable credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were fabricated. The Creative Commons Public Domain Dedication waiver(http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made bachelor in this commodity, unless otherwise stated.

Reprints and Permissions

About this article

Cite this article

Limasset, A., Cazaux, B., Rivals, Eastward. et al. Read mapping on de Bruijn graphs. BMC Bioinformatics 17, 237 (2016). https://doi.org/10.1186/s12859-016-1103-nine

Download citation

• Received: 09 December 2015

• Accepted: 26 May 2016

• Published: 16 June 2016

• DOI : https://doi.org/10.1186/s12859-016-1103-9

Keywords

• Read mapping
• De Bruijn graph
• NGS
• Sequence graph
• path
• Hamiltonian path
• Genomics
• Assembly
• NP-consummate

needhamentil1981.blogspot.com

Source: https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-016-1103-9

Share this post